Flocking matter
The term active matter refers to many-body systems in which the microscopic constituents are in some sense active or alive. This usually means that they have some mean of self-propultion and interact with each other in complicated non-reciprocal ways. Some examples of active matter are flocks of birds, herds of animals, schools of fish, swarms of instects, but also bacteria colonies, cell tissues, and even interacting robots.
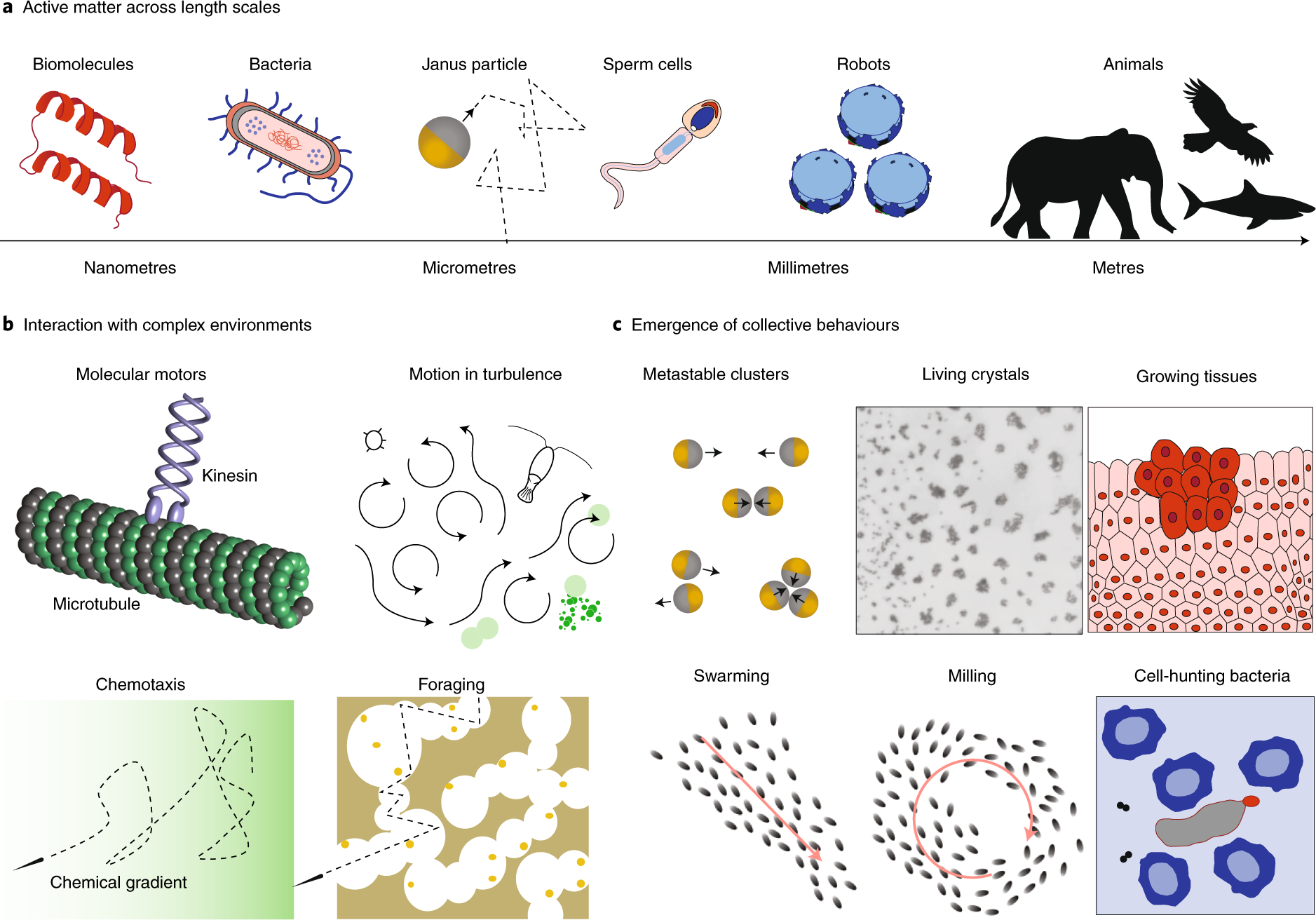
Active matter systems are very interesting to study because of their unusual features. Indeed, activity means that these systems are intrinsecally out-of-equilibrium, and therefore present characteristics which are very different to that of their passive counterparts. To name a few, active matter can develop unusual orders such as flocking, swarming, nematic, etc... while also presenting unusual density fluctuations.
In particular, I recently developed a strong interest in the flocking phase of dry active systems. This is characterized by the fact that, despite the lack of a designed leader, the various birds all start flying coherently pointing in the same direction. From a microscopic perspective, this is often modeled using the Vicsek model, which containts a list of rules that the microscopic agents follow to develop an emergent flocking behaviour.
However, flocking can also be described in terms of an effective hydrodynamic theory, valid at very long time and length scales. This has been put forward for the first time by Toner and Tu in 1998, who wrote an hydrodynamic theory for a velocity field \(\vec{v}\) and a number denisty \(n\). This theory presents a mechanism to spontaneously break rotations such that coherent motion arise even in two dimensions, showing that active matter systems can avoid the Merming-Wagner-Coleman theorem thanks to their out-of-equilibrium character, and furthermore is not Galilean-invariant (because the flock moves with respect to a medium). Despite its huge success in describing the flocking phase, the Toner and Tu model contains several phenomenological terms and there are still several open questions.
In (Amoretti et al., 2024) we arrived at two new results: first we showed that, despite their out-of-equilibrium features, the Toner and Tu equations can be completely recovered from the hydrodynamics of a passive fluid lacking boost symmetry (sometimes called boost-agnostic hydrodynamics in the literature). Secondly, grounding our argument on this fact, we suggested new exact scaling exponents that describe the long-scale dynamics of the hydrodynamic correlators and that are in excellent agreement with all previous known experiments and simulations of the Vicsek model.
Because our argument appears to be very robust, we are now trying to apply our ideas to different scenarios (Malthusian and incompressible flocks, quanched vs annehaled disorder, etc...). Furthermore, we are also thinking about ways to prove more formally the argument that allowed us to fix exactly the scaling exponents.

